LoRA

LoRA (Low Rank Adaptation) is a technique for minimizing the impact of fine tuning models.

Compared to GPT-3 175B fine-tuned with Adam, LoRA can reduce the number of trainable parameters by 10,000 times and the GPU memory requirement by 3 times.¹

Aside from the benefits in training speed and performance, LoRA makes it possible to deploy “weights as modules”, for a larger model that’s fine-tuned to be more accurate for specific tasks.

A traditional fine-tunning approach will update weights and record the difference in those weights ($\Delta W$). Instead, LoRA looks to decompose the model weights, using the intrinsinc rank hypothesis, which states that not all weights are as important.

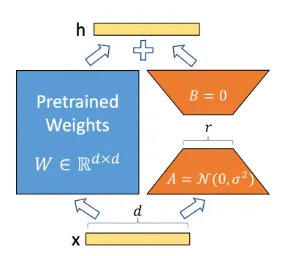
A full model is expressed by its weights ($W$), which fine-tunning decomposes in the original pre-trained weights and the deltas found in their fine tuned weights ($W=W_0+\Delta W$). At this point, the fine tuned weights $\Delta W$ has the same dimensions than the original model, but it could be very well decomposed into two matrices, $A$, and $B$, such that $\Delta W=AB$. If we consider $\Delta W$ to have dimensions $d\times k$, then we cannot choose these values, but we can choose a value $r$ and define the size of the new matrices such that $dim(A)=d\times r,dim(B)=r\times k$.

Finally, $A$ is initialized to a random Gaussian, and $B$ is initialized to zero, such that $W_0=0$, making no changes to the original model. Then, we freeze $A$ and just train on $B$.

Sources

• Understanding LoRA — Low Rank Adaptation For Finetuning Large Models
• microsoft/LoRA @ Github

Footnotes

1. LoRA: Low-Rank Adaptation of Large Language Models ↩