We’re going to assume that our solution to the model is a polynomial. Since we know that the solution to this relationship is a linear one, it’ll be a degree-1 polynomial, a line, of the shape . This implies that the solution is to find the right values for and that minimizes the objective function.
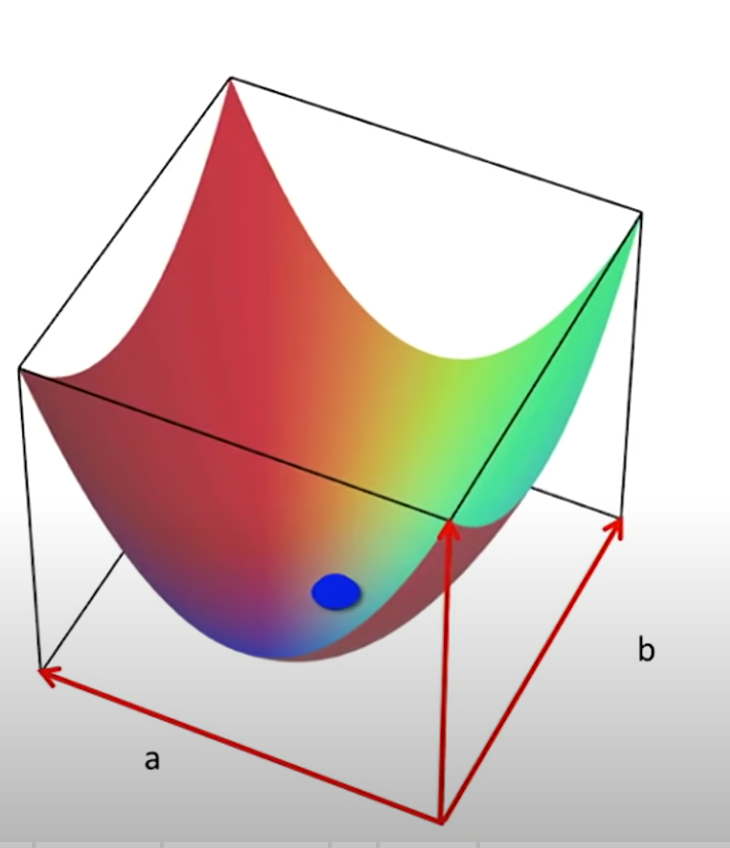
If we were to plot all the possible values for and and put a surface on it (in a third dimension), where the value of the objective function for that combination is the height of that surface, we can find the line that takes us from the top of that surface to the lowest point (through multiple steps). This is why the regression method is called linear regression, even if it’s used for higher-order polynomials.
And because the surface was produced as a sum of squares, we can guarantee that it has only one minimum.
We can use the values of the objective function to simply identify, quantitatively, how good the fit is, in relation to different models, as long as we’re using the same objective function.
Our goal is to model experimental data. Find a model that explains the phenomena of what we see, the underlying mechanism and make predictions about the behaviour in new settings. We need to account for noise and uncertainty in the data. Sometimes we have theories that might help, but sometimes we don’t. We still want to find the best models in those cases.
For models, we’re interested in polynomials, which are an easy way to model a curve that can help us predict values. This is because for polynomials, we only need to fit the coefficients that make it get close to the values that we want. This is called Linear Regression.
If we plotted the objective function (that we want to minimize, like the error), into the plane of possible coefficients, we’d get a shape that tell us the surface of the objective. A great feature of the sum-of-squares metric is that it will always give a concave shape.
For a polynomial of degree one, our coefficients are a and b:
Note that Linear Regression is about the method, so it is not limited to polynomials of degree 1.